Mit Vektoren lassen sich geometrische Objekt wie Geraden und Ebenen beschreiben. Dabei ergeben sich für Geraden und Ebenen verschiedene Darstellungsmöglichkeiten.
- Parameterform (für Geraden)
- Parameterform (für Ebenen)
- Normalenform (für Ebenen)
- Koordinatenform (für Ebenen)
- Hesse'sche Normalenform (für Ebenen)
Parameterform einer Geraden
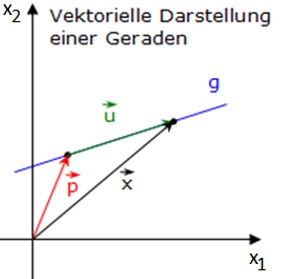
Eine Gerade bekommt man, indem man zu einem Punkt P auf der Geraden beliebige Vielfache eines Vektors addiert, der dieselbe Richtung wie die Gerade hat.
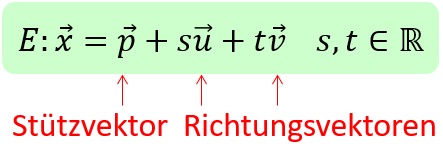
Damit erhält man die Parameterform:
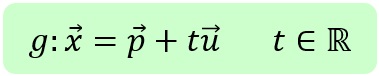
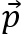nennt man den Stützvektor und
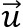den Richtungsvektor.
Das t ist der Parameter was den Namen dieser Darstellungsform erklärt.Beispiel:
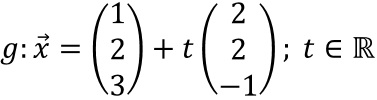
Aufgabe
Eine Gerade geht durch die Punkte A(1|4|4) und B(7|3|-1).
Ermitteln Sie eine Parameterform dieser Geraden.
Lösung
Verwende den Ortsvektor zu A als Stützvektor und den Verbindungsvektor von A nach B als Richtungsvektor.
Mit
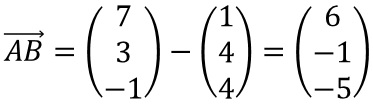folgt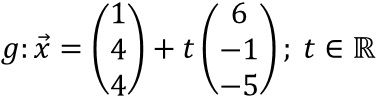 
.Parameterform einer Ebene
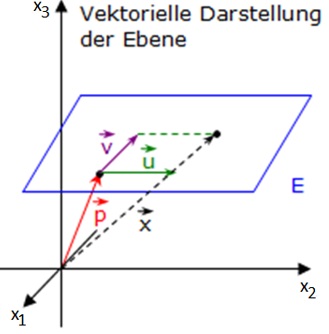
Wenn man der Parameterform einer Geraden einen zweiten (linear unabhängigen) Richtungsvektor hinzufügt, so erhält man die Parameterform einer Ebene. Ausgehend von einem Punkt auf der Ebene (der durch den Stützvektor beschrieben wird) kann man beliebige Vielfache der beiden Richtungsvektoren addieren und erreicht dadurch jeden beliebigen Punkt in der Ebene. Dadurch ist die Ebene komplett beschrieben.
Parameterform:
Beispiel:
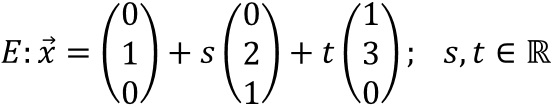
Aufgabe
Ermitteln Sie eine Parameterform der Ebene, die durch die Punkte A(2|6|-4), B(-2|3|2) und C(-4|3|4) geht.
Lösung
Wähle einen beliebigen Punkt, z.B. A, als Stützvektor. Gewöhnlich wählt man nun
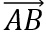und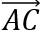 
als Richtungsvektoren.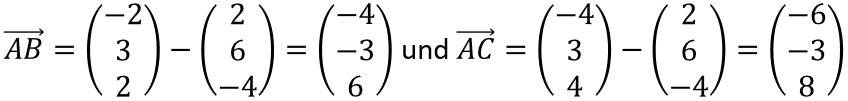
.
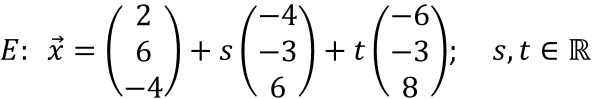| Downloads |
PowerPoint